Summary

The aim of my investigation was to look into the effect of various parameters on the functioning of solar cells made from various types of silicon.

In Experiment One, I investigated the effect of the intensity of light on the efficiency of solar cells. This showed that the amorphous and monocrystalline decreased in efficiency with an increase in intensity, whilst the polycrystalline cell increased its efficiency at higher intensities. Experiment Two showed some interesting aspects of the quantum nature of light and energy absorption, as at one wavelength (red) the cells were particularly effective, at the other wavelengths the cell produced very little energy. Experiment Three was an investigation into the effect of temperature on the output of solar cells. I found that the output was proportional to the temperature at constant intensity. Realisation of the limitations of the investigation and an interest in the possibilities of the introduction experimental of error in previous experiments led me onto experiments four and five. In Experiment Four I found that there was a slight difference between the mathematical prediction of what would happen to the output of the cell and what was observed, possible due to the different efficiency at lower intensity as shown in Experiment One.

Had I had time, I could have gone on to investigate the effect of temperature and angle on each of the cells, and the internal resistance of each. I could have also investigated the effect of a glass or plastic covering, like the amorphous and monocrystalline cells had, on the cell efficiency. All of the cells were partially protected from the weather, so testing the effect of water on all three of them could have been interesting too.

 

Contents

Section                                                           Page

Summary                                                        1

Contents                                                         1

Introduction                                                    2

Experiment 1                                                 3

Experiment 2                                                 8

Experiment 3                                                 12

Experiment 4                                                 16

Experiment 5                                                 18

                                   

 

Introduction

The relationships that I originally planned to investigate were:

1.      The relationship between the intensity of light falling on solar cells, and the power that they produce

I planned to vary the intensity using the inverse square law, as

intensity µ 1/d2, so varying the distance between the light source and the cell would vary the intensity.

2.      How effective they are in light of different wavelengths

I planned to do this by placing filters in between the bulb and the cell.

3.      How temperature affects them

I planned to do this by changing the temperature of the cell by placing the cell in a plastic bag and submerging it in water of a certain temperature, then removing it and quickly taking readings

Outline: I shone light onto the cells and measured the emf of the cell using a voltmeter, and the flow of current using an ammeter. The set-up that I used is described under the headings of each experiment. My original idea was to have a bulb sitting on a table, with a cell a certain distance away from it. The method was, however, modified differently to suit each experiment.

I will investigate three types of cells. Monocrystalline silicon cells are grown from a single crystal of silicon and are said to be the most efficient, polycrystalline silicon cells are made of many crystals grown, then crushed together and sliced thinly and are thus very cheap and thin. Amorphous silicon cells are made from amorphous silicon that has not been grown into special crystals and therefore is cheaper. The three cells will not be properly comparable against eachother in terms of power, because they are not the same thickness.

 

Experiment One

Investigating the effect of intensity on the power of solar cells

This experiment involves changing the intensity of light falling on different cells and measuring their power outputs. Higher intensity of light means that there are more photons hitting the surface of the cell per unit area per second. The more hit the cell, the more rapidly the electrons move across the p-n junction, so the larger the emf produced. If the rate of movement of electrons is inhibited, then the greater the rate of supply of photons (intensity), the more will not successfully excite an electron, so the lower the efficiency of the cell. I therefore predict that the higher the intensity, the greater the emf across the cell, the greater the power output of the cell, and the lower the efficiency of the cell.

Method

The intensity of the light falling on the cell will vary with the separation of the light source and the cell according to the inverse square law:

intensity µ 1/d2 so I can vary the intensity by changing the distance between the light source and the cell. I have calculated the amount of light hitting the cell by the ratio of area of the cell to the ratio of area over which light is spread:

intensity = power from bulb x surface area of cell

                                                            4 p r2

The power from the bulb was worked out from the current through the bulb and voltage put across it by the power pack. An estimated efficiency of 2% was used.

Outline: I varied the distance of the light source from the cell, then took readings from a voltmeter in parallel, and an ammeter in series, with the solar cell.

 Rough trials showed the following:

·        Text Box: Figure 1: The bulb Using the thin layer polycrystalline cell, I found that pressing contacts onto the surface of the cell scratched it, so I taped wire pickups onto the top and bottom with transparent tape, as shown on the pictures. I noticed that the readings obtained for the current produced by the cell were inconsistent between ammeters (see Experiment Five). I therefore changed my method for the amorphous and monocrystalline cells and used the voltage readings and the resistance of the voltmeter to work out the power output of the cell by P = V2/R.

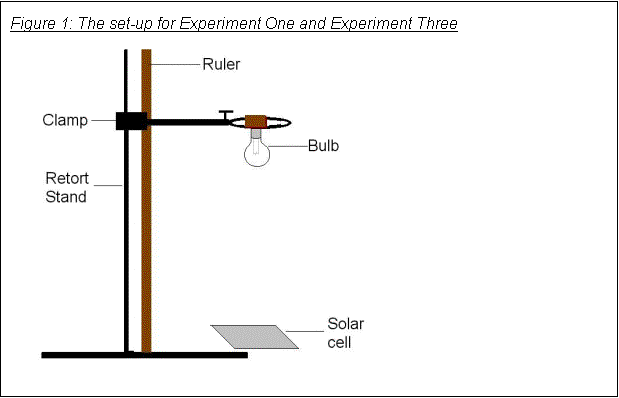
·        Having the cell and bulb standing on the table and changing the horizontal distance between them meant that the top and bottom of the cell got a different amount of light, and the distribution changed with distance. To ensure that the same amount of light was reaching each region of the cell (as near as possible), I held the bulb upside-down on a clamp stand, with the cell under it, as shown in Figure 2.

·        The easiest way to change the height of the bulb, was to draw a line around it with a felt pen at the same height as the filament, as shown in Figure 1. I then used the shadow projected onto the ruler taped to the retort stand to measure the height.

·        Text Box: Figure 2: The set-up for Experiment One and Experiment Three To ensure that the bulb was centred above the cell, I used a fabric tape measure to measure the distance from the line on the bulb to each corner of the cell.

The experiment set-up that I used is shown in Figure 2.

Results

The whole results analysis tables for Experiment One are included in Appendix 1.

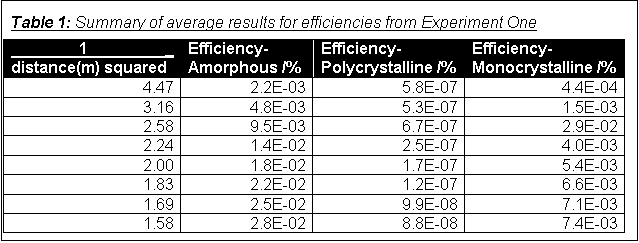
Table 1 is a summary of the results (averages) used to plot the graphs of the efficiencies of the three types of cell. The graph for the amorphous silicon cell is shown overleaf, the other two in Appendix 1. The result ringed with red on the graph is obviously an anomaly, so I repeated the experiment, and the result is ringed with purple on the graph. It is possible that the readings causing the anomaly were for 50 mm rather than 150 mm separation, but were entered in the table under 150 mm.

Text Box: Table 1: Summary of average results for efficiencies from Experiment One 1 _ distance(m) squared Efficiency- Amorphous /% Efficiency- Polycrystalline /% Efficiency- Monocrystalline /% 4.47 2.2E-03 5.8E-07 4.4E-04 3.16 4.8E-03 5.3E-07 1.5E-03 2.58 9.5E-03 6.7E-07 2.9E-02 2.24 1.4E-02 2.5E-07 4.0E-03 2.00 1.8E-02 1.7E-07 5.4E-03 1.83 2.2E-02 1.2E-07 6.6E-03 1.69 2.5E-02 9.9E-08 7.1E-03 1.58 2.8E-02 8.8E-08 7.4E-03


 



Error analysis

All measurements of distance taken during the experiment are with rulers accurate to 1mm. However, for the height of the cell, the shadow from the line drawn around the bulb was about 2mm thick, so the accuracy is estimated as +/- 0.004 m in column B of the results tables shown in Appendix 1. The voltmeter and ammeter used to measure the power output of the cell were accurate to 0.5 units, so the combined error of the voltage and current reading is estimated to be +/-1 for the power into the bulb. The digital multimeter was theoretically accurate to 0.01 units, but fluctuated during use as an ohmmeter so I estimated its accuracy to about one tenth of the value it was reading and rounded the value to the nearest integer, hence the value of 1E+07 for the resistance of the voltmeter and inaccuracy of +/- 1E+06. For the voltage (and current) readings, and the calculated efficiency, I used the deviation of my five readings to estimate the error. The error for the intensity of light falling on the cell (power into cell) was calculated by putting the values of error estimated for the distance, area etc. into the equation used to calculate the intensity of light. The calculated and estimated inaccuracies are shown on the results table in Appendix 1 and represented on the graphs in the form of error bars. Inclusion of constant errors like the bulb efficiency and the fact that the light is not spread out over a sphere due to the fact that part of the bulb was covered by the wooden base. I estimated these errors as about 20% and included them as error bars in the graphs.

Conclusion

The results show that, for monocrystalline and amorphous silicon cells the efficiency does indeed decrease with an increase in intensity. The effect that increasing the intensity had on the efficiency of the cell decreased as the intensity increased, resulting in a curved graph with asymptotes. The case for the polycrystalline is exactly the opposite- the efficiency increases with the light intensity and then plateaus out.

The reason that the amorphous and monocrystalline cell acted in this way could be due to the physical factors limiting the rate of conduction and the way in which boron-phosphorus p-n junctions work. If electrons can only move slowly, the number of electrons in the lowest filled band of the n-type semiconductor will depend on the rate at which electrons move to it and on the rate at which they are removed. If photons are supplied more quickly, this results in more electrons being excited and moving to the lowest unfilled band of a phosphorus atom, therefore less electrons in the lowest filled band as they are removed from here more quickly. Since there are fewer electrons available for photoexcitation, more of the photons hitting the cell will not successfully excite an electron, so the efficiency will be lower.

The reason that the thin-layer polycrystalline cell acted differently to the monocrystalline and amorphous cells could be due to the increase in conductivity of semiconductors with an increase in current flowing through them. The efficiency of the polycrystalline cell is lower than that of the other types of cells, even more so when the efficiency calculated with the same calculation as the other two cells (Efficiency 2 on the table) is considered. The low activity of these cells means that the number of electrons in the lowest unfilled band ready to be excited is never in short supply, so the drop in efficiency at higher intensities does not occur. Instead, the competing factor has an effect: p-n junctions become better conductors, the greater the current flowing through them, so the greater the intensity the better the cells are at causing a current to flow. The levelling-off of the graph could be due to the photon rate effect competing with this.

It should be noted that the V2/R method of calculating power and efficiency for the polycrystalline cell gave much smaller calculated power (see "Power out of cell" column on polycrystalline table in Appendix 1). This could be suggestive that the value measured for the resistance of the voltmeter is too high, therefore the real efficiency values being much larger. I therefore used V*I, as shown in "power out of cell 2"This does not, however, explain the fact that the amorphous cell came out as the most efficient cell. This high efficiency could be explained by the fact that the cell is smaller and its surface area harder to measure than the other cells, so the error may be the factor that causes this.

Experiment Two

Investigating the effect of the frequency of light on the output of the cell

This experiment involved shining light of different frequencies onto solar cells and measuring the emf produced across the cell, and current flowing. The better the absorbance of silicon matches the spectrum of light available from solar radiation, the better the cell will be.

Method

Text Box: Figure 3: The set-up for Experiment Two and Experiment Four The original plan was to place gels in-between the light source and the cell, but there were no gels available that would cover the whole bulb without white light leaking to the cell, and reducing amount of light falling on the cell would mean smaller readings so greater percentage inaccuracies. I therefore used a 35mm slide projector to shine light through 35mm slide filters of known wavelength. The set-up is shown in Figure 3. The wooden block is to keep the cell upright without obscuring it. The slide projector stood on a stack of paper to make it exactly the same height as the middle of the cell.

Light from the sun includes infrared and ultra-violet radiation too, so I briefly investigated whether this had an effect on the cell.

As the light was of low intensity, there was not enough light to see my book by. I therefore used a tray and a second power pack and bulb to create a light-shielded corner to take the readings. The second power pack was to prevent the second bulb interfering with the power output of the main bulb when used for the temperature experiments later on.

Text Box: Table 2: A summary of results for Experiment Two Wavelength Power for polycrystalline cell Power for amorphous silicon cell 620 8.21E-07 6.26E-07 595 3.4E-08 2.94E-07 550 4.6E-08 3.97E-08 495 866 7.50E-08 465 910 8.28E-08 415 510 2.60E-08 UV lamp yes emf produced I later discarded the data for the current due to the discrepancies with the different ammeters, but I used the "Power output of cell 2" column on the table in Appendix 2 for this experiment, leaving the values calculated by the V2/R method merely for comparative reference.

Results

The results used to plot the graphs shown overleaf are included in Table 2. The full results are in Appendix Two at the back of the report. The graph of wavelength against intensity for the polycrystalline and amorphous silicon cell is shown overleaf.

Error analysis

The biggest error in this experiment is the absorbance of the filters, which may be very different from eachother. Also significant is the difference between the light coming from the slide projector and the spectral distribution of normal sunlight. I realise that this changes for sunlight during the day, but there is a standard for testing solar cells, which is spectral distribution of AM 1.5, and adhering to this would have proven my experiment more valuable.  I have estimated the error involved in the wavelengths as +/- 10nm, as I have simply taken the approximate average of the wavelengths transmitted by the filters to plot on the graph. The inaccuracies for the measurements came from the accuracy and fluctuation of the apparatus, and the percentage inaccuracy of the power is estimated from the observed fluctuation within the results. I could not have calculated the inaccuracy in terms of +/- a number of watts, as the results range from 8.3E-07 to 1.5E-10, so I wrote them as a percentage.

Conclusion

The spread of frequencies at which the amorphous silicon cell absorbed light and produced a current appears to cover a much wider range than that of the polycrystalline cell (see previous pages). The monocrystalline silicon cell showed a even wider spread than the amorphous cell, but unfortunately the results for this went missing.

The amorphous cell appears therefore to be the better performer in terms of the range of light that it can utilise to convert to electricity. As all the cells are made of silicon, the p-type layer doped with boron and the n-type layer with phosphorus, they should absorb the same frequencies. I think that the differences may be due to that which covers the layers of silicon. The polycrystalline cell is coated with titanium dioxide anti-reflective coating. TiO2 can itself be used together with amorphous organic crystalline substances to create very efficient cells so may have an effect. The amorphous cell has a plastic sheaf, and the monocrystalline cell is coated in glass, which is probably of special anti-reflective nature. The various anti-reflective coatings and coverings may either absorb light itself (as in the case of TiO2) or change the frequency of the light by absorbing one frequency and fluorescing another, as some semi-conductors can. For example, semi-conductors made from aluminium, gallium, indium and phosphorus can absorb blue light and re-emit orange light. As I am not sure about the nature of the glass covering on the monocrystalline cell, this may be the secret to its larger absorption spectrum.

Experiment Three

Investigating the effect of temperature on the output of the polycrystalline cell

In this experiment, I investigated the effect of the temperature of the cell on its output. Temperature affects semiconductors in a way that it affects no other material: they are semiconductors because at room temperature there is sufficient energy to thermally excite some of the electrons, thus giving them a slight charge-carrying capacity and making them semi-conductors. The important thing about this is that doping the semiconductor with atoms that have more or less outer-shell electrons will increase or decrease the number of electrons available to carry charge significantly and have a huge effect on the conductivity of the semiconductor. Another important result of this is that their conductivity varies with temperature. I therefore predict that they will perform better at higher temperatures. I have not tried the other two cells due to the time-consuming nature of the experiment, and I would expect the results to be the same for all cells anyway.

Method

In my original method I planned to put the cell in a water-proof plastic bag and submerge it in water of various temperatures, but:

·        Heating it up by submerging it in water of different temperatures proved to be rather tricky, as the cell cooled down (or warmed up) to room temperature very quickly once it had been taken out of the water and its bag. I therefore used a hairdryer to control the temperature above room temperature. I tried a cold-air hair dryer, but this did not get the temperature as low as I wanted to take measurements, so I used an ice-pack to lay on to the cell to cool it down.

·        I found that the normal glass thermometers were not suitable, as:

Ĝ      They only have a small bulb at the end of the thermometer which actually does most of the temperature detection

Ĝ      The relatively large diameter of the glass outer means that heat would be lost (or gained) on the upper side of the thermometer, resulting in an untrue temperature reading

Ĝ      It would involve leaning over the cell to read of the temperature, then quickly looking on the voltmeter

I tried a fever strip thermometer, as this would be in intimate contact with the cell, but this is only accurate to two significant figures, has a very small temperature range, and approximate colour-related reading. I therefore used a LogIt box to measure the temperature, which has a reading to three significant figures from zero to 110 degrees Celsius. This is more suitable as it:

Ĝ      Has a gauge the same length as the cell

Ĝ      Has a reading to three significant figures

Ĝ      Is long and thin so it is in close contact with the cell, and the reading should be close to that of the cell

Ĝ      Has an extension lead, so the display screen can be next to the voltmeter.

·        I found that it was not possible to keep the cell at a constant temperature, it fluctuated constantly, and the ice-pack method could not be regulated- it was simply a method of leaving it on and taking measurements at whatever temperature the LogIt box read. It was therefore not possible to take a reading for both current and voltage, as the temperature would have changed in-between. I therefore used the voltage V reading and the resistance R of the voltmeter to work out the power P of the cell by P = V2/R.

I took measurements both while the cell was heating up and while it was cooling down, so that I could be sure that any effect was not produced by the bulb heating up and emitting more or different frequency light as time proceeded. The set-up that I used is shown in Figure 2.

Results

The full results are in Appendix 3 at the back of the report.

I have drawn a graph with the data from run 1, run 2, and run 3, and this is shown overleaf. I have included a computerised graph of all the data in Appendix 3 for clarity. It does not include a trend line for run 6, as I did not see good enough correlation to do so. The computer got the trend line wrong for run 3 of the experiment; this should be parallel to the trend line for run 2.

Error analysis

The biggest error affecting this experiment was the time lag between the cell changing temperature and the probe detecting the new temperature. This is shown by the fact that the lines on the graph overleaf have different gradients depending on how quickly they changed temperature and whether it was a loss or gain of heat. The results for run 6 were taken whilst the cell was heating up and cooling down alternately, and there is no correlation because the temperature I recorded was related to what the temperature had been, and not what it was, so changing the direction of temperature change meant that the time lag was essentially reduced, then created in the other direction. I have not included error bars on the graph that I drew by hand, because I am not sure what this error is, and the graph would have got very messy if I had. The computerised version in Appendix 3 includes error bars for the error in the apparatus of about +/- 0.1V and +/- 0.1 K. The time lag was estimated to be about +/- 5%, and was included as error bars in the X-axis direction. The results boxed in red on the table (run 1) in Appendix 3 are not plotted, as they are obviously anomalies.

 

Conclusion

The relationship appears to be linear, hence

Emf across cell µ temperature

Emf = k x temperature

The graph below shows that the experiments each had a different value for k, perhaps due to the fact that there was a time-lag between the cell actually being at a particular temperature and the LogIt reading being that temperature, as the probe must first come into thermal equilibrium with the cell to be correct, which never happens as the cell is constantly changing temperature. The reason for this increase in power output is the increase in thermal conductivity due to the fact that more electrons are thermally excited and have left their silicon atom at higher temperatures. Although, when tested in experiment two, the cell did not produce a current with an infrared lamp in the absence of visible light, this experiment has shown that temperature nevertheless has an effect.

Experiment Four

Investigating the effect of the angle of incidence on the relative power output of the polycrystalline silicon cell

The nature of the experiment meant that the light was reaching the cell at different angles on different regions of the cell. In a real situation, the light reaching the cell would consist of parallel sunlight, diffuse light scattered by the particles in the atmosphere, and reflected light from the surroundings. This led to an interest in investigating the effect of this, other than mathematical, on the power output of the cell. Also, as I was carrying out the investigation, I realised that if the angle affected the utilisation of the light, this could have an even larger effect on my results than the dispersion of light and consequent uneven distribution over the surface of the cells. This could mean that, not only were the smaller cells getting more intense light, but if the angle from which it came mattered, the results for the high efficiency of the amorphous cell in Experiment One might well be explained. I therefore set about to find out whether there was any such affect.

Method

This experiment involves changing the angle of the cell relative to the direction of the light. I found that the easiest way to do this is using the set-up shown in Figure 3. This is because the light coming from the slide projector is more focused in one direction than that from the bulb. I photocopied a board protractor onto a piece of A3 paper and stuck this to a piece of cardboard. I then affixed a needle to the middle of the cell and pushed the needle into the middle of the protractor baseline, so that the cell pivoted on the needle without moving away from its central position. That way the cell always stayed the same distance from the light, as the two sides of the cell always moved in opposite directions.

The projector would only project if there was a slide in it, so I cut a piece of cardboard the same shape as a slide without glass and used this to keep the lens open.

Results

Text Box: Table 3: The averages of my results for Experiment Four Angle to normal Power output of cell 0 3.47E-10 10 3.19E-10 20 2.82 E-10 30 2.48E-10 40 1.94E-10 50 1.25E-10 60 6.53E-11 70 2.06E-11 80 9.61E-12 90 0 With normal being at 90° to the direction of the light, Table 2 is a summary of the averages of my results.

This is the one experiment where I got readings when there was no direct light shining on the cell. This was due to the high intensity light from the projector reflecting off the walls and around the room. I have, however, entered it as zero on the table.

A graph of the table on the left is shown in Appendix Four, along with a graph of the effect of the angle on the intensity of the light falling on the cell.

 

 

Error analysis

As I was using a large photocopy of a protractor, I estimated the error in measuring the angle to be +/- 2 degrees. The voltage readings deviated from each other by about +/- 1 mV. The deviation of the results for the calculated power deviated by about 1E-10. The error on the Y-axis was too small to show on my graph, but the X-axis error is shown. A graph with both the measured powers and the predicted line is shown on a single graph for comparison in Appendix Four.

Conclusion

This experiment shows a small link between the angle and the power output of the cell, even when the power output is compared to the graph of the effect of the angle on the intensity of the light falling on the cell. This is done be the equation

Cos q = __adjacent__

               hypotenuse

Part of the difference between the mathematical and the actual graph could be due to the varying efficiencies at different intensities.. It is the shape of a Y = mX4 + nX3 + oX2 +pX type graph. I am, however, more inclined to believe that its shape is simply caused by factors such as shadows cast by the pickups as the angle changes, the change in the amount of light reflected due to the grain of the polycrystalline cell, or the distribution of the light in the beam of the projector, so that the middle has little light, then there is a stronger ring, then it starts getting weaker again and then stronger still. This seems the most likely explanation for the observation, although there may be some amazing phenomenon at work here. It would have been interesting, time permitting, to have investigated this for all three types of cells, but the results went missing and it was not possible to take them again.

Experiment Five

Investigating the internal resistance of the polycrystalline cell

As mentioned in Experiment One, I tested several ammeters for how much current they said the cell was producing, and they all gave different readings. Some were different by a factor of ten, or even a hundred. Results are shown in Table 3.

Text Box: Table 4 Ammeter Reading/mA Digital multimeter 1 52.5 Digital multimeter 2 200.8 Analogue grey meter with mA shunt 65.8 Digital ammeter 2000 Large mA ammeter 20.75 8MK II 80.4 I put this down to the internal resistance of the cell and ammeter, and the different methods of measuring used by different ammeters. I therefore decided to use the voltage and resistance method for the rest of the investigation. When I tested the different voltmeters, they all read the same emf across the cell. This is probably because the internal resistance is not comparable with that of the voltmeters- the resistance of the voltmeter that I tested was about 10MW.

The points discussed above led me to investigating the internal resistance of the cells. My method is explained below.

Method

As

e = V+v

So

e = IR + Ir

V = -Ir + e

Where V is the voltage dropped across the resistor, v is the voltage dropped across the internal resistance, e is the electromotive force of the cell and R and r are the resistance of the resistor and the internal resistance consecutively. I is the current flowing in the circuit. The last equation is in the form y=mx+c, so if a graph of voltage against current is drawn, the gradient is the internal resistance and the point where the graph meets the y-axis is the emf of eh cell. By changing the resistance in the circuit, one can change the amount of current that flows through, and the voltage across, the cell. I therefore wired up a variable resistor in series with the cell and an ammeter, and a voltmeter in parallel across the cell. I changed the variable resistor to known values and recorded the current in the circuit and the PD across the cell.

I had to calibrate the resistor because the values stated on the box were not accurate. I therefore used the real measured values in my calculations.

Results

All the results are shown in Appendix Five. A graph of the current against the voltage is shown overleaf. I took three readings of current and averaged them, using the average to draw the graph.

Error analysis

The error in the voltage measurement was limited by the apparatus and fluctuations to +/- 0.3V. The X-axis error was about +/- 0.1A due to apparatus, and is too small to show on the graph overleaf.

Conclusion

The graph shows some correlation, but the scale was not accurate enough to get a real value for the internal resistance of the cell. Maybe this was because the resistances used were too high to compare with the internal resistance of the cell, so the voltage drop was not noticeably redistributed when R became large, as r is very small and therefore the voltage drop v due to the internal resistance too small to have an effect. The internal resistance may still, however, be comparable with that of the ammeters, thereby causing the suspected problems.

 

 

 

Appendices

In this section are the full data analysis tables and the less significant graphs

Notes:

·        The number of the appendix corresponds to the experiment whose data it contains

·        The columns are labelled to make showing the equations used to analyse the data easier

The dependant variables that I measured for Experiment One are shown in bold.

| HOME | INDEX |
| CHEMISTRY | BIOLOGY | PHYSICS | GERMAN |
| ABOUT ME | LINKS | WWW PAGE | EMAIL ME |